Component analysis#
An introduction to component analysis in phasor space.
Import required modules, functions, and classes:
import math
import matplotlib.animation as animation
import numpy
from matplotlib import pyplot
from phasorpy.components import (
phasor_component_fit,
phasor_component_fraction,
phasor_component_graphical,
)
from phasorpy.phasor import phasor_from_lifetime
from phasorpy.plot import PhasorPlot, plot_histograms
numpy.random.seed(42)
component_style = {
'linestyle': '-',
'marker': 'o',
'color': 'tab:blue',
'fontsize': 14,
}
Fractions of two components#
The phasor coordinates of combinations of two lifetime components lie on the line between the two components. For example, a mixture of:
Component A: 1.0 ns lifetime, 60% contribution
Component B: 8.0 ns lifetime, 40% contribution
frequency = 80.0 # MHz
component_lifetimes = [1.0, 8.0] # ns
component_fractions = [0.6, 0.4]
component_real, component_imag = phasor_from_lifetime(
frequency, component_lifetimes
)
plot = PhasorPlot(frequency=frequency, title='Fractions of two components')
plot.components(
component_real,
component_imag,
component_fractions,
labels=['A', 'B'],
**component_style,
)
plot.show()
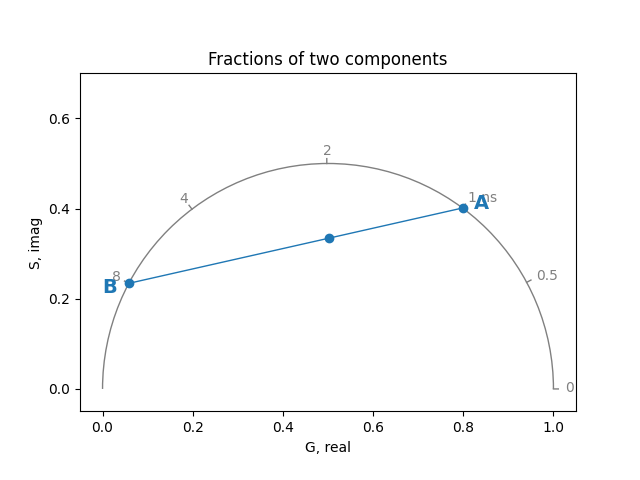
If the location of both components is known, their contributions (fractions) to the phasor point that lies on the line between the components can be calculated:
real, imag = phasor_from_lifetime(
frequency, component_lifetimes, component_fractions
)
fraction_of_first_component = phasor_component_fraction(
real, imag, component_real, component_imag
)
assert math.isclose(fraction_of_first_component, component_fractions[0])
Distribution of fractions of two components#
Phasor coordinates can represent different contributions from two components with known phasor coordinates:
real, imag = numpy.random.multivariate_normal(
(real, imag), [[5e-3, 1e-3], [1e-3, 1e-3]], (100, 100)
).T
plot = PhasorPlot(
frequency=frequency, title='Distribution of fractions of two components'
)
plot.hist2d(real, imag, cmap='Greys')
plot.components(
component_real, component_imag, labels=['A', 'B'], **component_style
)
plot.show()
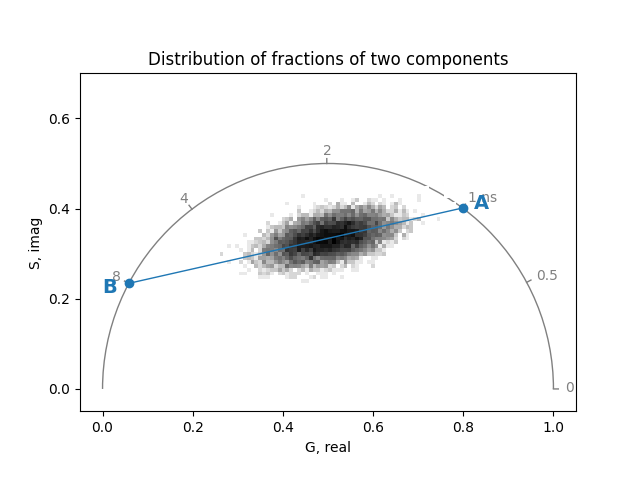
When the phasor coordinates of two contributing components are known,
their fractional contributions to phasor coordinates can be calculated by
projecting the phasor coordinate onto the line connecting the components.
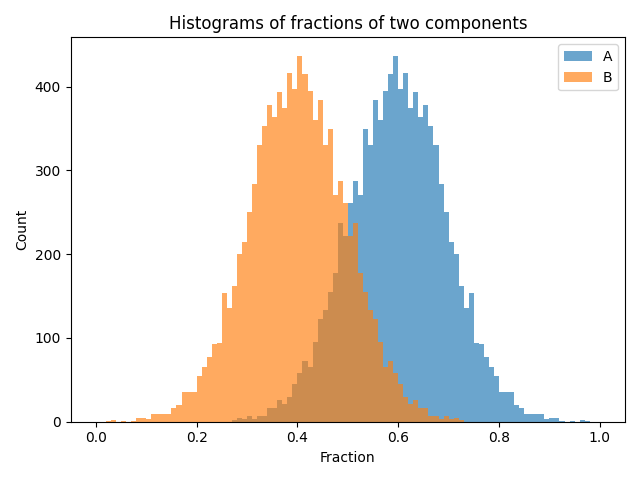
Fractions are calculated using
phasorpy.components.phasor_component_fraction()
and plotted as histograms:
fraction_of_first_component = phasor_component_fraction(
real, imag, component_real, component_imag
)
plot_histograms(
fraction_of_first_component,
1.0 - fraction_of_first_component,
range=(0, 1),
bins=100,
alpha=0.66,
title='Histograms of fractions of two components',
xlabel='Fraction',
ylabel='Count',
labels=['A', 'B'],
)
Multi-component fit#
When the phasor coordinates of multiple contributing components are known, their fractional contributions to phasor coordinates can be obtained by solving a linear system of equations, using multiple harmonics if necessary.
Fractions of 2 components are fitted using
phasorpy.components.phasor_component_fit()
and plotted as histograms:
fraction1, fraction2 = phasor_component_fit(
numpy.ones_like(real), real, imag, component_real, component_imag
)
plot_histograms(
fraction1,
fraction2,
range=(0, 1),
bins=100,
alpha=0.66,
title='Histograms of fitted fractions of multiple components',
xlabel='Fraction',
ylabel='Count',
labels=['A', 'B'],
)
Up to three components can be fit to single harmonics phasor coordinates. The Multi-component fit tutorial demonstrates how to fit 5 components using two-harmonics.
Graphical analysis of two components#
The phasorpy.components.phasor_component_graphical()
function for two components counts the number of phasor coordinates
that fall within a radius at given fractions along the line between
the components.
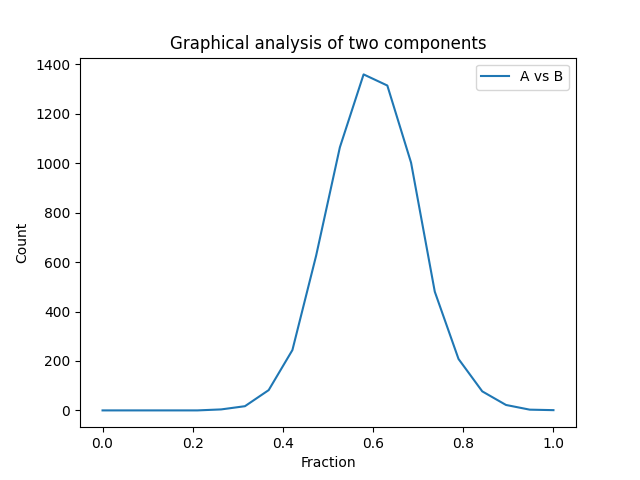
Compare the plot of counts vs fraction to the previous histogram:
radius = 0.025
fractions = numpy.linspace(0.0, 1.0, 20)
counts = phasor_component_graphical(
real,
imag,
component_real,
component_imag,
fractions=fractions,
radius=radius,
)
fig, ax = pyplot.subplots()
ax.plot(fractions, counts[0], '-', label='A vs B')
ax.set_title('Graphical analysis of two components')
ax.set_xlabel('Fraction')
ax.set_ylabel('Count')
ax.legend()
pyplot.show()
Graphical analysis of three components#
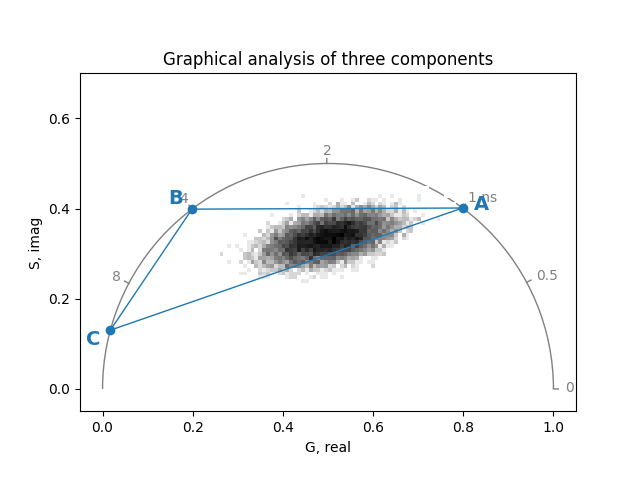
The graphical method can similarly be applied to the contributions of three components:
component_lifetimes = [1.0, 4.0, 15.0]
component_real, component_imag = phasor_from_lifetime(
frequency, component_lifetimes
)
plot = PhasorPlot(
frequency=frequency, title='Graphical analysis of three components'
)
plot.hist2d(real, imag, cmap='Greys')
plot.components(
component_real, component_imag, labels=['A', 'B', 'C'], **component_style
)
plot.show()
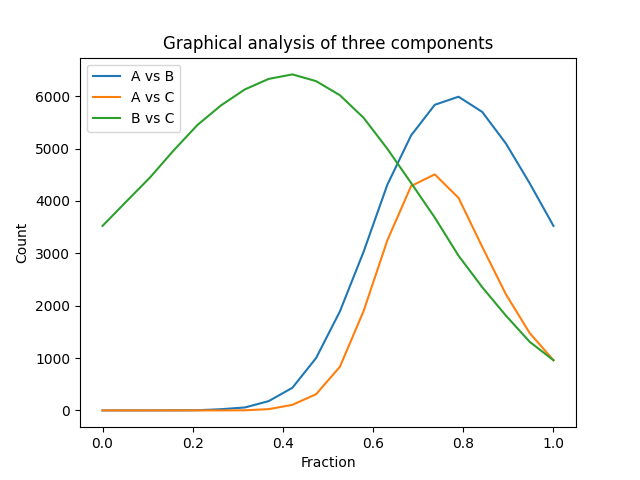
The results of the graphical component analysis are plotted as histograms for each component pair:
counts = phasor_component_graphical(
real,
imag,
component_real,
component_imag,
fractions=fractions,
radius=radius,
)
fig, ax = pyplot.subplots()
ax.plot(fractions, counts[0], '-', label='A vs B')
ax.plot(fractions, counts[1], '-', label='A vs C')
ax.plot(fractions, counts[2], '-', label='B vs C')
ax.set_title('Graphical analysis of three components')
ax.set_xlabel('Fraction')
ax.set_ylabel('Count')
ax.legend()
pyplot.show()
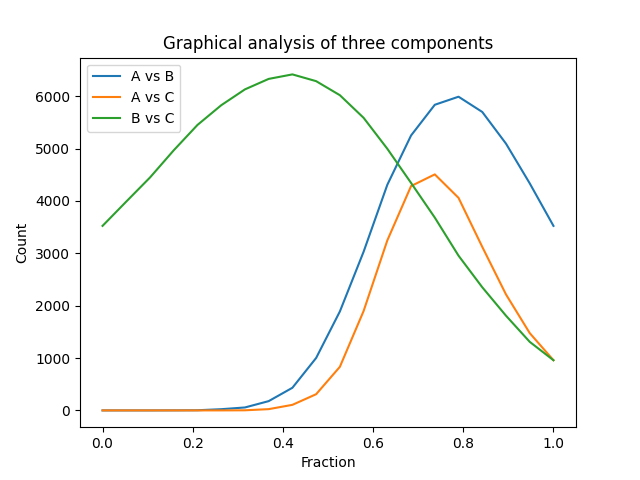
The graphical method for resolving the contribution of three components (pairwise) to a phasor coordinate is based on the quantification of moving circular cursors along the line between the components, demonstrated in the following animation for component A vs B. For the full analysis, the process is repeated for the other combinations of components, A vs C and B vs C:
fig, (ax, hist) = pyplot.subplots(nrows=2, ncols=1, figsize=(5.5, 8))
plot = PhasorPlot(
frequency=frequency,
ax=ax,
title='Graphical analysis of component A vs B',
)
plot.hist2d(real, imag, cmap='Greys')
plot.components(
component_real[:2],
component_imag[:2],
labels=['A', 'B'],
**component_style,
)
plot.components(
component_real[2], component_imag[2], labels=['C'], **component_style
)
hist.set_xlim(0, 1)
hist.set_xlabel('Fraction')
hist.set_ylabel('Count')
direction_real = component_real[0] - component_real[1]
direction_imag = component_imag[0] - component_imag[1]
plots = []
for i in range(fractions.size):
cursor_real = component_real[1] + fractions[i] * direction_real
cursor_imag = component_imag[1] + fractions[i] * direction_imag
plot_lines = plot.plot(
[cursor_real, component_real[2]],
[cursor_imag, component_imag[2]],
'-',
linewidth=plot.dataunit_to_point * radius * 2 + 5,
solid_capstyle='round',
color='red',
alpha=0.5,
)
hist_artists = pyplot.plot(
fractions[: i + 1], counts[0][: i + 1], linestyle='-', color='tab:blue'
)
plots.append(plot_lines + hist_artists)
_ = animation.ArtistAnimation(fig, plots, interval=100, blit=True)
pyplot.tight_layout()
pyplot.show()
sphinx_gallery_thumbnail_number = 6 mypy: allow-untyped-defs, allow-untyped-calls mypy: disable-error-code=”arg-type”
Total running time of the script: (0 minutes 5.654 seconds)